Vnútorný opis SAR
Vnútorný opis vlastností systémov v čase
Opis systémov:
- Vonkajší opis systému
Vyjadruje vzťahy len medzi výstupnou a vstupnou veličinou. Systém považujeme za „čiernu skrinku“, tzn. nezaujíma nás obsah skrinky. Skúmame len reakciu výstupu na vstupné podnety.
- Vnútorný opis systému – stavový
Je to vyjadrenie dynamických vlastností systému vzťahmi medzi vstupom, výstupom a stavom systému. Je vyjadrený stavovými rovnicami. Stavový opis sa v kybernetike používa najmä pre opis riadených objektov.
Pracujeme s pojmom stav systému, čo je súhrn všetkých veličín systému (okrem vstupných), ktoré vieme do opisu zahrnúť a matematicky vyjadriť. Sú to napríklad všetky prúdy a napätia v elektrickom systéme, alebo poloha, rýchlosť a zrýchlenie v systéme mechanickom. U lietadla to môžu byť kurz, sklon, náklon, výška a ich derivácie, teda rýchlosti (prípadne uhlové rýchlosti) a zrýchlenia. Stavový opis podáva významne väčšie množstvo informácie o správaní daného systému, než opis vonkajší (kde poznáme iba reakciu na výstupe). Preto sa používa v moderných, kvalitatívne vyšších (lepších) systémoch riadenia, kde riadiaci systém musí pracovať s informáciami o stave riadeného objektu a bez nich by také (dokonalé riadenie) nebolo vôbec principiálne možné – viď napríklad dnes už bežné vektorové riadenie asynchrónnych motorov.
Výhodou stavového opisu je aj to, že je formálne rovnaký pre jednorozmerové aj viacrozmerové systémy (systémy s viacerými vstupnými – akčnými aj výstupnými veličinami), čo je napríklad aj lietadlo, kde základnými akčnými veličinami sú výchylka kormidiel (krídielka, stabilizátor (výškovka) a smerovka a výstupy sú kurz, sklon, náklon, výška a podobne.
Pod stavom systému rozumieme vnútornú charakteristiku systému, hodnota ktorej v určitom okamihu t určuje hodnotu výstupnej veličiny v tom istom čase t, za predpokladu, že poznáme hodnotu vstupnej veličiny v tomto čase t a v predchádzajúcom časovom intervale (histórii, ktorá sa ešte v správaní systému prejavuje).
Vstupné a výstupné veličiny v matematickom modeli systému vyjadrujú pôsobenie prostredia na objekt a objektu na prostredie a majú určitý fyzikálny význam. Stavové veličiny musia opisovať vnútorný stav systému tak, aby umožňovali jednoznačne opísať procesy, ktoré prebiehajú v danom objekte. To znamená, že umožňujú napísať jednoznačne vzťahy medzi vstupnými, stavovými a výstupnými veličinami. Jedným zo spôsobov, ako je možné opísať vnútorný stav systému, je maticový opis:
| $ \mathbf{\dot{x}(t)}= \mathbf{A(t)}.\mathbf{x(t)} + \mathbf{B(t)}.\mathbf{u(t)} $ $ \mathbf{y(t)}= \mathbf{C(t)}.\mathbf{x(t)} + \mathbf{D(t)}.\mathbf{u(t)} $ |
(1) |
Prvá z uvedených rovníc je stavová rovnica a druhá výstupná rovnica.
Všetky veličiny v opise sú vektory, pričom:
-
Vektor $ \mathbf{x} $ je vektorom stavových veličín systému (vektor vnútorného stavu) a môžeme ho napísať v tvare:
| $ \mathbf{x(t)}= \left[ \matrix{x_1(t)\\ x_2(t)\\ x_3(t)\\ \vdots\\ x_n(t)} \right] $ | (2) |
Jednotlivé zložky vektora $ \mathbf{x} $ môžu predstavovať napríklad polohu, rýchlosť a zrýchlenie riadeného objektu (RO).
-
Vektor $ \mathbf{u} $ – vstupný vektor, pre riadený objekt teda vektor akčných veličín:
| $ \mathbf{u(t)}= \left[ \matrix{u_1(t)\\ u_2(t)\\ u_3(t)\\ \vdots\\ u_r(t)} \right] $ | (3) |
V prípade jednorozmerového systému má vektor iba jednu súradnicu, napríklad $ u_1 $ .
-
Vektor $ \mathbf{y} $ – výstupný vektor:
| $ \mathbf{y(t)}= \left[ \matrix{y_1(t)\\ y_2(t)\\ y_3(t)\\ \vdots\\ y_m(t)} \right] $ | (4) |
Matice $ \mathbf{A(t)} $, $ \mathbf{B(t)} $, $ \mathbf{C(t)} $ a $ \mathbf{D(t)} $ (pre stacionárne systémy len $ \mathbf{A} $, $ \mathbf{B} $, $ \mathbf{C} $, $ \mathbf{D} $, teda matice z konštantných prvkov) v stavovej a výstupnej rovnici sú:
-
$ \mathbf{A} $ – matica vlastnej dynamiky
| $ \mathbf{\dot{x}(t)}= \mathbf{A(t)}.\mathbf{x(t)} $ | (5) |
Ak sa systém nachádza v určitom stave, tento vnútorný stav sa môže meniť aj bez pôsobenia vstupov. Opisuje teda dynamiku systému (vlastný pohyb).
Matica $ \mathbf{A(t)} $ má rozmer ($ n $x$ n $), kde $ n $ je rozmer stavového vektoru (počet jeho súradníc).
-
$ \mathbf{B} $ – budiaca matica systému
| $ \mathbf{\dot{x}(t)}= \mathbf{B(t)}.\mathbf{u(t)} $ | (6) |
Do zmeny stavu opisovaného systému pridávame pomocou tejto matice vplyv vstupnej veličiny. Vyjadruje, ako zmenu stavu spôsobujú vstupné (budiace) veličiny. V prípade obecného viac rozmerového systému je aj táto matica ($ n $x$ n $), ale pri menšom počte vstupných (akčných) veličín ako je počet veličín stavových sa počet jej stĺpcov redukuje. Napríklad pre jednorozmerný vstupný vektor „$ \mathbf{u} $“ má aj budiaca matica iba jeden stĺpec (ostatné stĺpce by nedávali žiadny zmysel, pretože by násobili súradnice vektora akčných veličín s nulovou hodnotou – nemôžeme riešiť odozvu na neexistujúce vstupy).
-
$ \mathbf{C} $ – výstupná matica
| $ \mathbf{y(t)}= \mathbf{C(t)}.\mathbf{x(t)} $ | (7) |
Keď vieme, aký je vnútorný stav systému, dostávame sa pomocou tejto matice k vyjadreniu výstupu (na výstup). Výstupná matica vyberá jednu alebo kombináciu stavových veličín, ktoré určujú výstup. Napríklad ak je daná výstupná rovnica:
| $ \mathbf{y}= \left[ \matrix{1 & 0 & 0} \right] \left[ \matrix{x_1\\ x_2\\ x_3} \right] $, | (8) |
vyberáme maticou $ \mathbf{C} $ za výstup $ y $ zložku (súradnicu) stavového vektora (napríklad polohu, aj keď v stavovom vektore vieme aj rýchlosť a zrýchlenie).
V prípade výstupnej rovnice:
| $ \mathbf{y}= \left[ \matrix{1 & -1& 0} \right] \left[ \matrix{x_1\\ x_2\\ x_3} \right] $, | (9) |
vyberáme za výstup riešeného objektu rozdiel súradníc stavového vektora $ x_1 - x_2 $ , (napríklad pre vyjadrenie napätia v diagonále mostíka pomocou napätí v jej uzloch).
-
$ \mathbf{D} $ – matica nezotrvačných (bezinerčných) väzieb
Objaví sa nenulová u systémov s nezotrvačnými vlastnosťami, kde opisuje priamu – okamžitú rekciu na výstupe. Opisuje vlastnosti systémov, ktoré sa správajú tak, že ak sa zmení vstupný signál (vektor) skokom, systém reaguje aj na výstupe okamžitou zmenou $ \mathbf{D}. \mathbf{u} $ (ku ktorej sa až v ďalšom čase pridáva postupná, cez stavové správanie systému – teda vyše opísaná zložka výstupu).
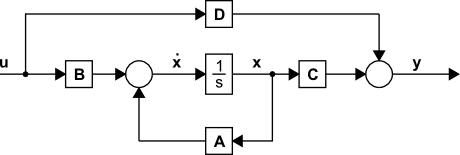
$ \mathbf{\dot{x}(t)}= \mathbf{A(t)}.\mathbf{x(t)} + \mathbf{B(t)}.\mathbf{u(t)} $
$ \mathbf{y(t)}= \mathbf{C(t)}.\mathbf{x(t)} + \mathbf{D(t)}.\mathbf{u(t)} $
Obr. 1.1 Obecná štruktúra systémov riešených stavovým opisom
Príklady vonkajšieho a vnútorného opisu jednorozmerových systémov a prevodov medzi nimi pomocou programovej schémy:
Pomocou zostavenia programovej schémy pre riešenie diferenciálnej rovnice metódou postupnej integrácie (ktorú môžeme priamo použiť pre modelovanie vlastností systémov, napríklad pomocou Simulinku) je možné ukázať zostavenie stavovej a výstupnej rovnice pre daný systém:
Príklad 1
Systém druhého rádu je opísaný vonkajším opisom diferenciálnou rovnicou
| $ a_2 \mathbf{\ddot{y}} + a_1 \mathbf{\dot{y}} + a_0 \mathbf{y} = b_0 \mathbf{u} $. | (10) |
Po úprave:
| $ \mathbf{\ddot{y}} = - \dfrac {a_1} {a_2} \mathbf{\dot{y}} + \dfrac {b_0} {a_2} \mathbf{u} - \dfrac {a_0} {a_2} \mathbf{y} $. | (11) |
môžeme vyjadriť vzťah pre riešenie systému metódou postupnej integrácie a zakresliť programovú schému:
| $ \mathbf{y} = \int - \dfrac {a_1} {a_2} \mathbf{y} + \iint \dfrac {b_0} {a_2} \mathbf{u} - \iint \dfrac {a_0} {a_2} \mathbf{y} $. | (12) |
Programová schéma určená pre daný systém vyše uvedeným vzťahom je znázornená na obrázku. (Je priamo použiteľná pre Simulink)
Obr. 1.2 Programová schéma jednorozmerového spojitého lineárneho dynamického systému druhého rádu
Keď do programovej schémy vyznačíme stavové premenné „$ \mathbf{x} $“, je možné túto schému prepísať do maticových rovníc zodpovedajúcich stavovému, teda už vnútornému opisu systému:
| $ \left[ \matrix{\dot{x}_1\\ \dot{x}_2} \right] = \left[ \matrix{-a_1/a_2 & 1\\ -a_0/a_2 & 0} \right] \left[ \matrix{x_1\\ x_2} \right] + \left[ \matrix{0\\ b_0/a_2} \right] \left[ \matrix{u\\0} \right] $ $ y = \left[ \matrix{1 & 0} \right] \left[ \matrix{x_1\\ x_2} \right] $ |
(13) |
Určili sme tak súčasne všetky matice vnútorného stavového opisu riešeného systému (nenulové $ \mathbf{A} $, $ \mathbf{B} $, $ \mathbf{C} $ a nulová matica $ \mathbf{D} $ – riešený systém je zotrvačný).
Príklad 2
Podobným postupom riešime systém opísaný diferenciálnou rovnicou tretieho rádu:
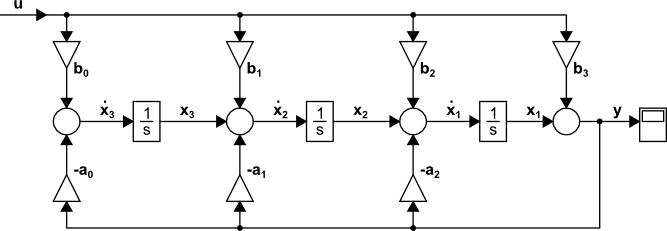
| $ \mathbf{\dddot{y}} + a_2 \mathbf{\ddot{y}} + a_1 \mathbf{\dot{y}} + a_0 \mathbf{y} = b_3 \mathbf{\dddot{u}} + b_2 \mathbf{\ddot{u}} + b_1 \mathbf{\dot{u}} + b_0 \mathbf{u} $ $ \mathbf{\dddot{y}} = b_3 \mathbf{\dddot{u}} + b_2 \mathbf{\ddot{u}} - a_2 \mathbf{\ddot{y}} + b_1 \mathbf{\dot{u}} - a_1 \mathbf{\dot{y}} + b_0 \mathbf{u} - a_0 \mathbf{y} $ $ y = b_3 u + \int \left( b_2 u - a_2 y \right) dt + \iint \left( b_1 u - a_1 y \right) dt^2 + \iiint \left( b_0 u - a_0 y \right) dt^3 $ |
(14) |
Obr. 1.3 Programová schéma spojitého lineárneho dynamického systému tretieho rádu
Po zápise stavových veličín do schémy je možný jej prepis na stavové rovnice:
| $ \left[ \matrix{\dot{x}_1\\ \dot{x}_2 \\ \dot{x}_3} \right] = \left[ \matrix{-a_2 & 1 &0 \\ -a_1 & 0 & 1 \\ -a_0 & 0 & 0} \right] \left[ \matrix{x_1 \\ x_2 \\ x_3} \right] + \left[ \matrix{ b_2 -a_2 b_3 \\ b_1 -a_1 b_3 \\ b_0 -a_0 b_3} \right] \left[ \matrix{u \\0 \\0} \right] $ $ y = \left[ \matrix{1 & 0 & 0} \right] \left[ \matrix{x_1 \\ x_2 \\ x_3} \right] + b_3 u$ |
(15) |
V druhej rovnici sa objavuje člen $ b_3u $, teda matica $ \mathbf{D} $ obsahuje nenulový prvok $ b_3 $, pretože ide o nezotrvačný systém (čo sme už vedeli na základe zhody rádu derivácií vstupného a výstupného signálu v zadanej diferenciálnej rovnici).
Kanonické tvary stavových rovníc
Osobitný význam majú kanonické tvary stavových rovníc. Využívajú sa najmä pri opise jednorozmerových systémov pre určenie stavového opisu bez potreby programovej schémy (teda priamo a efektívne).
Ako vieme, jednorozmerový stacionárny lineárny systém môžeme opísať jednou diferenciálnou rovnicou v tvare:
| $ \sum_{i=0}^n a_i y ^{(i)}(t) = \sum_{j=0}^m b_j u^{(j)}(t) $ | (16) |
Predpokladajme, že $ a_n $=1 a $ m $<$ n $, teda že systém je zotrvačný, $ \mathbf{D} $=0. Uvedenú diferenciálnu rovnicu môžeme nahradiť ekvivalentným systémom diferenciálnych rovníc a algebraickou rovnicou, ktoré budú stavovými - maticovými rovnicami systému:
| $ \mathbf{\dot{x}(t)}= \mathbf{A(t)}.\mathbf{x(t)} + \mathbf{b(t)}.\mathbf{u(t)} $ $ \mathbf{y(t)}= \mathbf{C}^T.\mathbf{x(t)} $ |
(17) |
Pri modelovaní systémov a pri analýze a syntéze systémov riadenia sa často využíva jeden zo základných tvarov kanonický , kde matica $ \mathbf{A} $ a vektor $ \mathbf{b} $ a $ \mathbf{C}^T $ majú tvar:
| $ \mathbf{A} = \left[ \matrix{0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \\ -a_0 & -a_1 & -a_2 & \cdots & -a_{n-1}} \right] $ $ \mathbf{b} = \left[ \matrix{0 \\ 0 \\ \vdots \\ 0 \\1} \right] $ $ \mathbf{C}^T = \left[ \matrix{\\ b_0 & b_1 & \cdots & b_m & 0 & \cdots & 0} \right] $ |
(18) |
Matica $ \mathbf{A} $ má rozmer ($ n $x$ n $), $ \mathbf{b} $ má rozmer (1x$ m $) a $ \mathbf{C}^T $ má mať rozmer ($ n $x1) a nie vždy platí, že $ n $=$ m $, za členy $ b_0-b_m $ sa dopíše toľko núl, aby platilo, že $ n $=$ m $.
Iný tvar kanonických rovníc (líši sa spôsob zápisu matíc $ \mathbf{A} $, $ \mathbf{B} $ a $ \mathbf{C} $) je:
| $ \mathbf{A} = \left[ \matrix{0 & 0 & \cdots & 0 & -a_0\\ 1 & 0 & \cdots & 0 & -a_1\\0 & 1 & \cdots & 0 & -a2\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 1 & -a_{n-1}} \right] $ $ \mathbf{b} = \left[ \matrix{b_0 \\ b_1 \\ \vdots \\ b_m \\0 \\ \vdots \\0} \right] $ $ \mathbf{C}^T = \left[ \matrix{\\ 0 & 0 & \cdots & 0 & 1} \right] $ |
(19) |
Aj v tomto prípade má matica $ \mathbf{A} $ rozmer ($ n $x$ n $), no vektor $ \mathbf{C}^T $ má rozmer ($ m $x1) a vektor $ \mathbf{b} $ má mať rozmer (1x$ n $), preto sa za členy $ b_0-b_m $ sa dopíše toľko núl, aby platilo, že $ n $=$ m $.
Ako je vidieť aj v uvedených príkladoch, kanonické tvary stavových rovníc sa vyznačujú minimálnym počtom nenulových prvkov a zároveň minimálnym počtom prvkov rôznych od nuly a jednotky v matici $ \mathbf{A} $ a vo vektoroch $ \mathbf{C}^T $ a $ \mathbf{b} $.
Zadanie príkladu: systém určený diferenciálnou rovnicou v predchádzajúcom príklade č.1 opíšte stavovým opisom pomocou obidvoch uvedených kanonických tvarov.
- prečítané 5962x